Introduction
Due to limited stiffness, a 4th order system or in other words mechanical systems are characterized by internal resonances which limit dynamical performance, both open-loop and closed-loop. To study the impact of this behavior, a simplified model known as the 4th-order system or 2-mass-spring-damper system is often used. This lumped model is often a good representation for the low-frequent behavior of real-world motion systems.
4th-order system
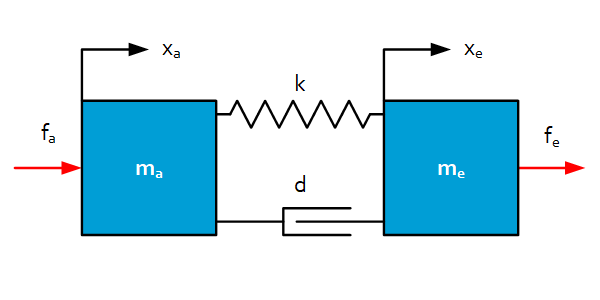
The system consists of 2 masses, connected with a spring and damper. In analogy with a real motion system, the first mass is connected to the actuator of the system (a), whereas the second mass represents the end-effector (e), the functional part of the system. The flexibility in between both parts can represent a complex drivetrain or just a monolithic interconnection.
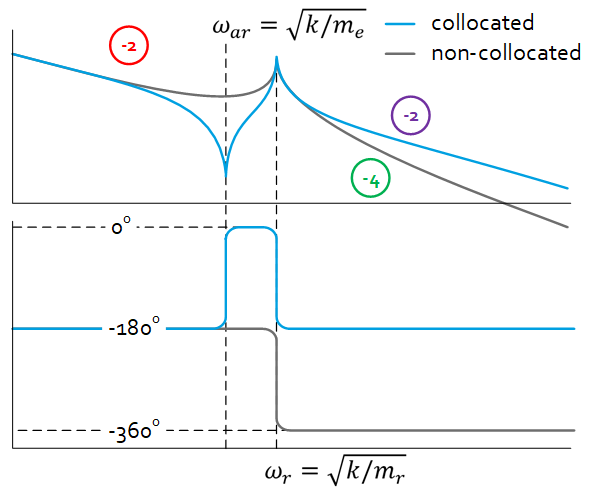
Collocated in words
The transfer from a motor force to the motor body position, known as collocated transfer. This transfer is of importance for feedback control design if the position sensor is located on the actuator side. At low frequencies the bode plot shows a -2 slope, which is inertia behavior of both masses. Above the resonance frequency $\omega_r$ only the mass of the motor is sensed on that position. The mass of the end-effector head is “decoupled” at those frequencies. At the dip in the frequency response, the anti-resonance $\omega_{ar}$, the motor force makes the end-effector mass shake while the motor is approximately standing still. Therefore this frequency is approximately equal to the single mass-spring resonance of the end-effector.
Collocated in formulae
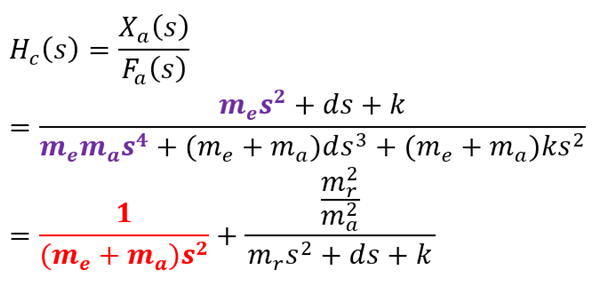
Non-collocated in words
The transfer from motor force to end-effector position, referred to as non-collocated. If the sensor mounted close to the end-effector, this is the plant transfer. It shows a -4 slope for frequencies above $\omega_r$, which means the end-effector is not following the displacement of the motor anymore.
Non-collocated in formulae
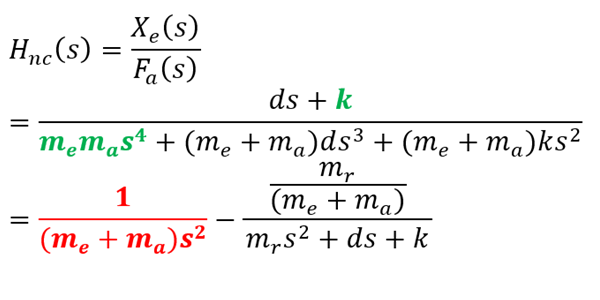
$m_r=\frac{m_em_a}{{(m}_e+m_a)}$ is the modal mass of the internal resonance mode.
