Introduction
In many applications it is relevant to know the total connection stiffness of an object in relation to a given reference. In many cases there are several stiffness paths which introduces the need to calculate the ‘equivalent’ stiffness. This is a single stiffness representing the sum of all individual stiffness’ in the appropriate way, taking into account the series/parallel configuration and possible movement amplifications/reductions. Below a number of cases is listed.
| Case | Equivalent stiffness |
|---|---|
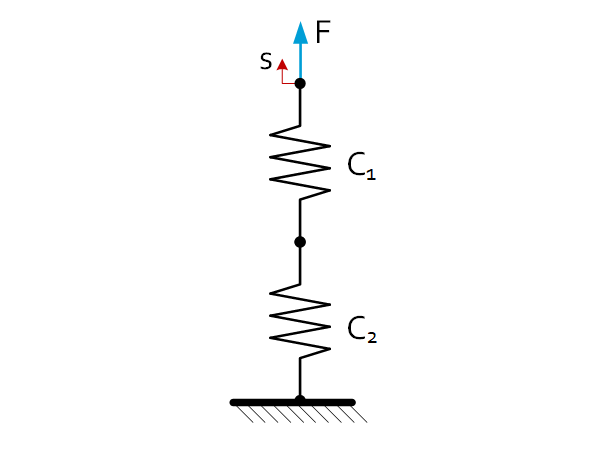 | $C_{eq}=\frac{F}{s}=\frac{C_1\cdot C_2}{C_1+C_2}$ |
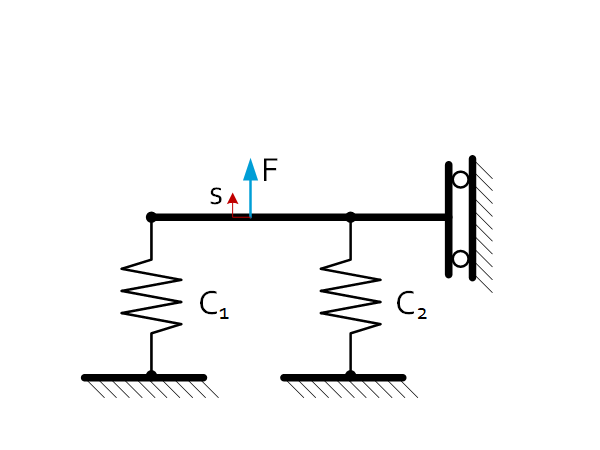 | $C_{eq}=\frac{F}{s}=C_1+C_2$ |
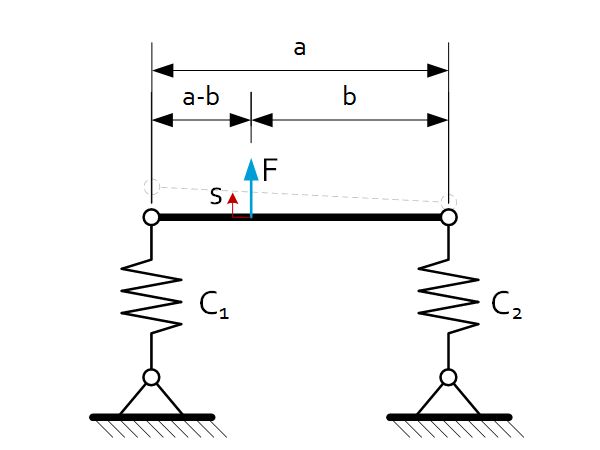 | $C_{eq}=\frac{F}{s}=\frac{a^2\cdot C_1\cdot C_2}{\left(a-b\right)^2\cdot C_1+b^2{\cdot C}_2}$ |
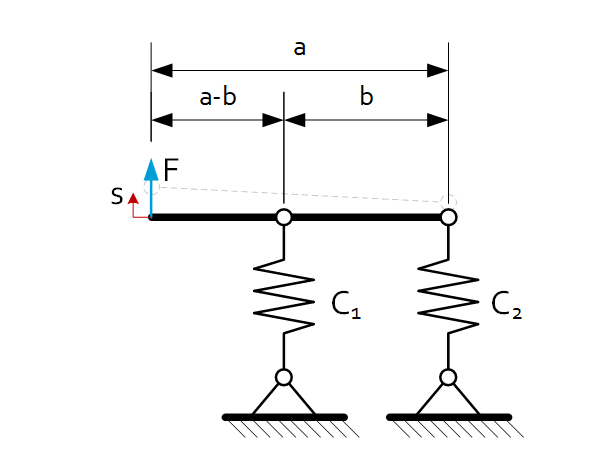 | $C_{eq}=\frac{F}{s}=\frac{b^2\cdot C_1\cdot C_2}{\left(a-b\right)^2\cdot C_1+a^2{\cdot C}_2}$ |
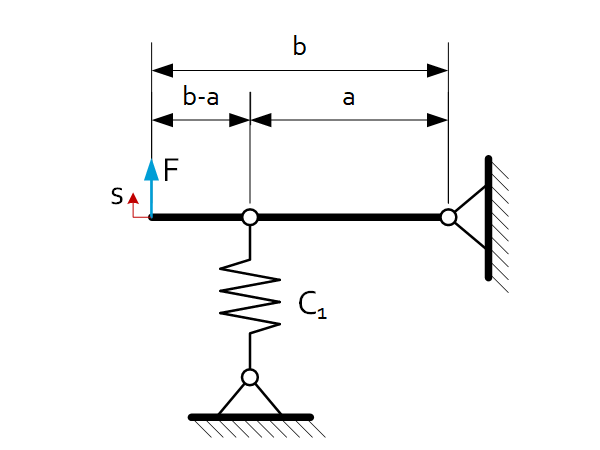 | $C_{eq}=\frac{F}{s}=\left(\frac{a}{b}\right)^2\cdot C_1=i^2\cdot C_1$ |
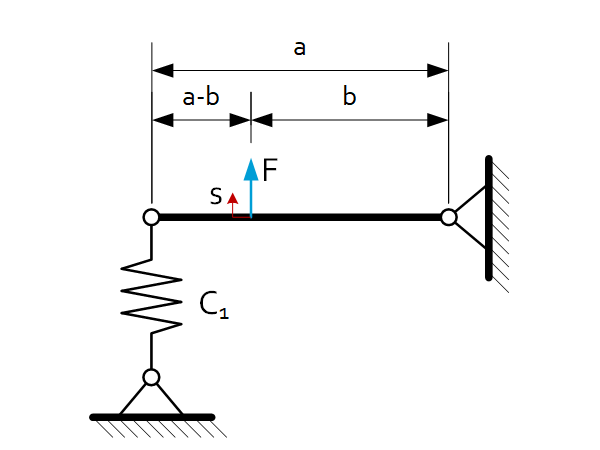 |
|
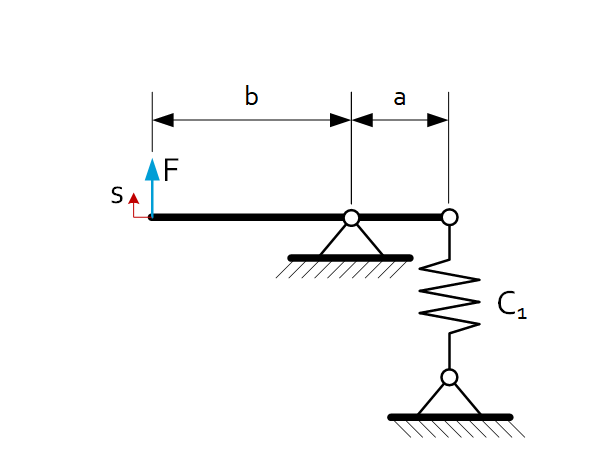 |
|
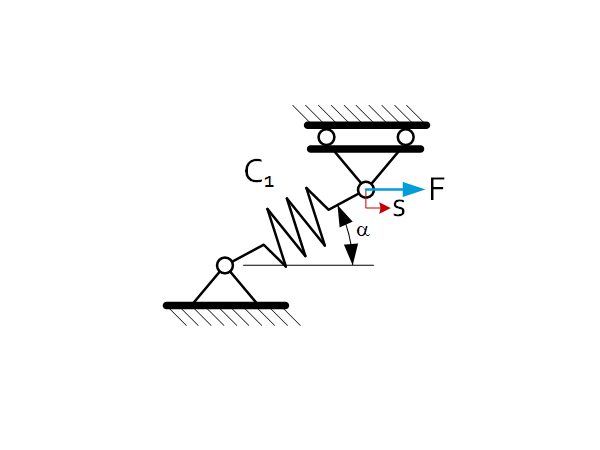 | $C_{eq}=\frac{F}{s}=\cos^2{\alpha}\cdot C_1$ |
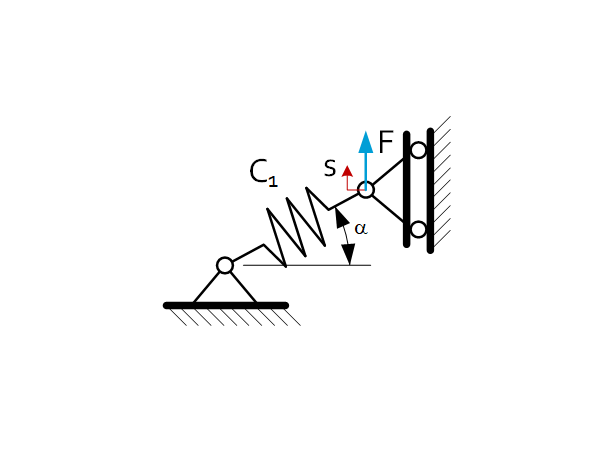 | $C_{eq}=\frac{F}{s}=\sin^2{\alpha}\cdot C_1$ |
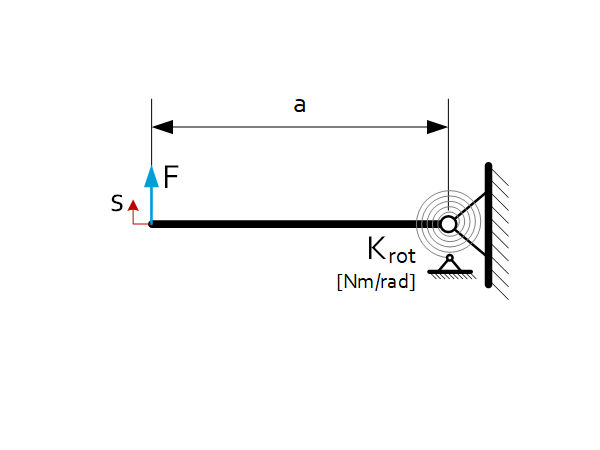 | $C_{eq}=\frac{F}{s}=\frac{K_{rot}}{a^2}$ |
