Introduction
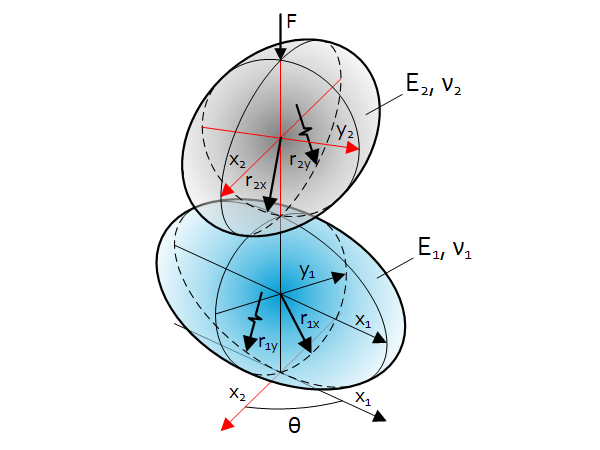
Universal calculation of Hertz point contact between two arbitrarily curved bodies in the shape of two ellipsoids under load $F$ and each body has radii around the x and y axis of which the smallest radius is called $r_x$ and the largest is called $r_y$. For a convex shape the radii are positive, for a concave shape the radii are negative and for a plane both radii are infinite. The alignment of the bodies around the Z-axis is defined by $θ$. Further parameters of the bodies are the Young’s modulus and Poisson’s ratio.
To simplify further calculations, the rather complex geometry of two ellipsoids at an angle is expressed in the equivalent relative curvature $R_e$ and the ratio of the curvature radii $\varepsilon_{rr}$. The combination of different materials is simplified by using the equivalent Young’s modulus $E_r$.
Equivalent Young’s modulus
$E_r=\left(\frac{{1-v}_1^2}{2E_1}+\frac{{1-v}_2^2}{2E_2}\right)$
Note: for metals $\nu\approx0.3$, so the equivalent Young’s modulus for metal on metal contact is:
$E_r\approx2.2\frac{E_1E_2}{E_1+E_2}$
Support variables
To keep equations readable the support variables $P,\ Q,\ r_x^\prime$ and $r_y^\prime$ are introduced.
$P=\frac{1}{2}\left(\frac{1}{r_{1x}}+\frac{1}{r_{1y}}+\frac{1}{r_{2x}}+\frac{1}{r_{2y}}\right)$
$Q=\frac{1}{2}\sqrt{a^2+b^2+2ab\cos{\left(2\theta\right)}}$
with $a=\frac{1}{r_{1x}}-\frac{1}{r_{1y}}$ and $b=\frac{1}{r_{2x}}-\frac{1}{r_{2y}}$
$r_x^\prime=\frac{1}{P+Q}$
$r_y^\prime=\frac{1}{P-Q}$
In the case that body 2 is in contact with a flat surface ($r_{1x},\ r_{1y}=\infty$) the $P$ and $Q$ equations can be simplified to:
$P=\frac{1}{2}\left(\frac{1}{r_{2x}}+\frac{1}{r_{2y}}\right)$
$Q=\frac{1}{2}\sqrt{\left(\frac{1}{r_{2x}}-\frac{1}{r_{2y}}\right)^2}$
Equivalent relative curvature
The physical interpretation of the equivalent relative curvature is: $R_e$ is the radius of a sphere on a plane, that would result in the same contact area as the actual contact between the ellipsoids.
$R_e=\sqrt{r_x^\prime r_y^\prime}$
Ratio of the curvature radii
The ratio of the curvature radii expresses the ratio between the relative curvatures, and it relates to the out of roundness (or ellipticity) of the contact. For a circular contact it has a value of 1, at very high values the contact will approach a line contact. Up to values of 800 the equations on this page can be used, for higher values equations for a rectangular contact should be used.
$\varepsilon_{rr}=\frac{r_y^\prime}{r_x^\prime}$
Ratio of the curvature radii correction factors
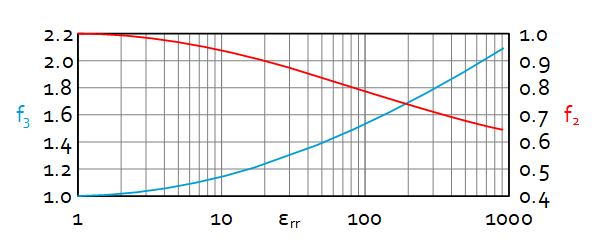
The stress, deformation and stiffness not only depend on the load and contact size but also on the ellipticity of the contact, to implement this dependence two correction factors $f_2$ and $f_3$ are used which are a function of $\varepsilon_{rr}$:
Deformation
$\delta=\sqrt[3]{\frac{9F^2}{4E_r^2R_e}}f_2$
Stress
$\sigma_{max}=\sqrt[3]{\frac{3FE_r^2}{2\pi^3R_e^2}}f_3$
Stiffness
The stiffness of the contact changes depending on the load, the average stiffness is then:
$C_{avg}=\frac{F}{\delta}$
The local stiffness is:
$C_{local}=\frac{dF}{d\delta}=\frac{3}{2f_2}\sqrt[3]{F\frac{4E_r^2R_e}{9}}$
Sphere on flat surface – rules of thumb
- Ball contact area: circular.
- For large stiffness use large radius, e.g. by using a segment instead of complete ball.
Convex roller on flat surface – rules of thumb
- Convex roller contact area: elliptical.
- Keep convex roller radius $r_{2y}$ max 25 times larger than $r_{2x}$. Larger ratios imply a line contact.
- For large stiffness use large roller radius, e.g. by using a segment instead of complete roller.
