Introduction
Every part of a mechanical system, from actuator to end-effector, comprises damping. This sheet gives an overview of ways damping can be defined and how these definitions are related to the linear dimensionless damping coefficient $\zeta$.
What is damping?
Damping in mechanical systems is the extraction of mechanical energy from the motion in the system, usually by conversion of potential energy into heat. Therefore it can be regarded as a loss of energy. However, the positive effect of damping is that it attenuates oscillations due to internal resonances. Damping is often modeled as a dissipation force proportional to the velocity, $F=d\dot{x}$, which is known as viscous damping. However the underlying principle is more complex and nonlinear in nature.
Damping ratio
A frequently used measure for damping in a system is the damping ratio. It characterizes the damping in a linear second-order system as the ratio of physical damping coefficient $d$, over the critical damping coefficient $\zeta=\frac{d}{d_c}$ with $d_c=2m\sqrt{\frac{c}{m}}$. This corresponds with the level of damping that the response becomes non-oscillatory. Note that this is a linear definition of damping, for which a model of the underlying system is needed.
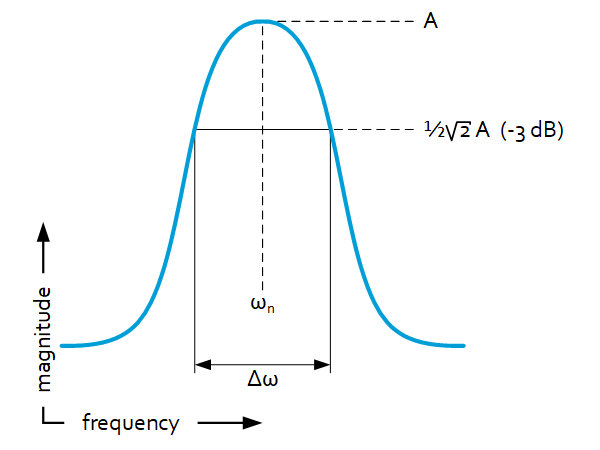
Q factor
Another interpretation of damping is given by the quality or Q factor, which is more widely used in other fields of physics. It is a measure for how under-damped the system is. It can be retrieved from frequency-response data:
$Q=\frac{\omega_n}{\Delta\omega}$
Another interpretation of Q is the rate of energy loss relative to the stored energy in the resonating system:
$Q=\omega_n\frac{energy\ stored}{power\ loss}$
It relates to the damping ratio by $\zeta=\frac{1}{2Q}$.
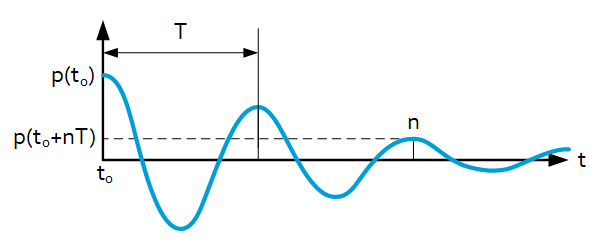
Logarithmic decrement
Damping ratio can be retrieved from resonant time-response data by means of the logarithmic decrement $\Lambda$, which can be calculated from the amplitude of peak responses:
$\Lambda=\frac{1}{n}\ln{\frac{p(t)}{p(t+nT)}}$
The damping ratio is calculated by:
$\zeta=\frac{1}{\sqrt{1+\left(\frac{2\pi}{\Lambda}\right)^2}}$
This method becomes inaccurate for large damping values, i.e. $\zeta>0.5$.
Dissipation factor
The dissipation factor (DF), which is often expressed as a percentage, is the reciprocal of the Q factor:
$DF=\frac{1}{Q}$
Exponential attenuation / decay rate
Often called attenuation $\alpha$, is defined as $\alpha=\zeta\omega_n$ [rad/s], which represents the exponential decay of the oscillation.
Loss angle
By applying a harmonic load F to a system, the response (deflection x), is known as the loss angle, which is a measure for damping. It relates to the damping ratio by $\zeta=\frac{\tan{\delta}}{2}$.
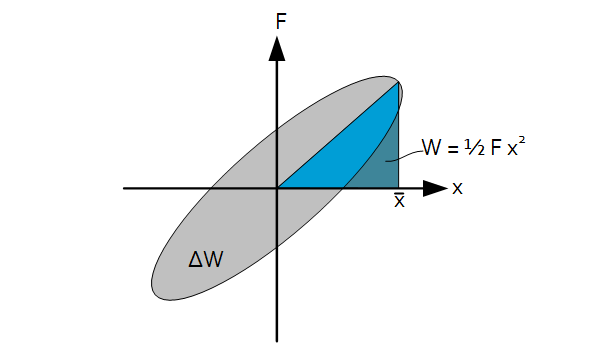
Specific damping capacity
By dividing the amount of energy dissipated in a harmonically excitated structure divided by the work applied to it, the specific damping capacity $\Lambda$ can be calculated:
$\psi=\frac{\Delta W}{W}$, $\zeta=\frac{\psi}{4\pi}$
The interpretation of this measure can be clarified by means of the hysteresis curve: