Introduction
Mounting thin lenses to their mechanical interfaces comprises imperfections to the initially designed optical paths due to manufacturing and assembly tolerances.
Quantification
This sheet provides qualitative information about the phenomena because derivation of the shifts and tilts of the image as a result of the lens and/or object movement is extensive and non-transparent.
Initial conditions
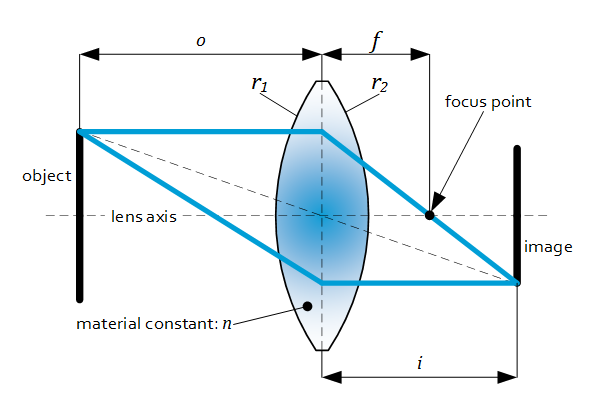
$f$
= focal length (average)
$n$
= refractive index of lens (medium air/vacuum: $n_m=1$)
$r_1,r_2$
= incoming radius, outgoing radius
$o,i$
= object distance, image distance
Focus distance $f$, object $o$ and image $i$ distance: $\frac{1}{f}=\frac{1}{i}+\frac{1}{o}$
Magnification: $m\ =\frac{i}{o}$
Lens x = object -x
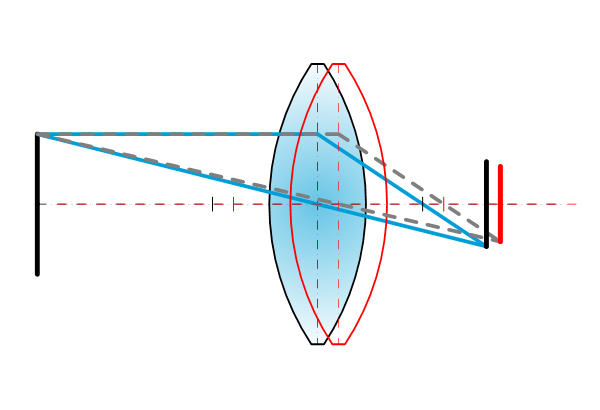
Lens y = object -y
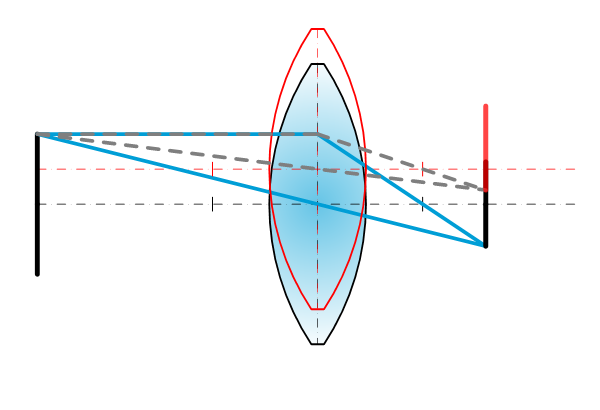
Lens tilt
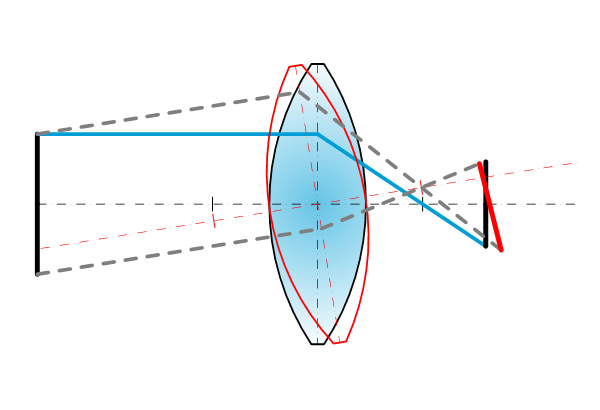
Object tilt
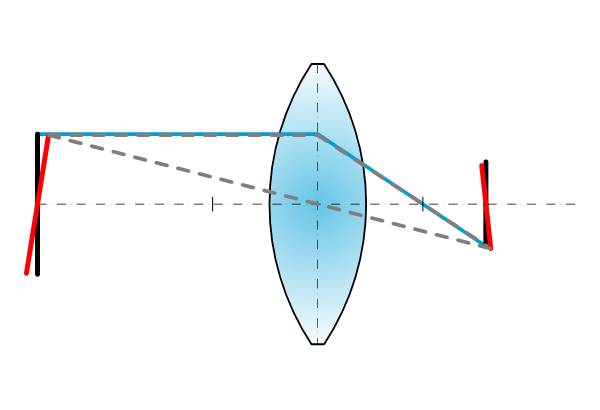
Lens y + lens tilt
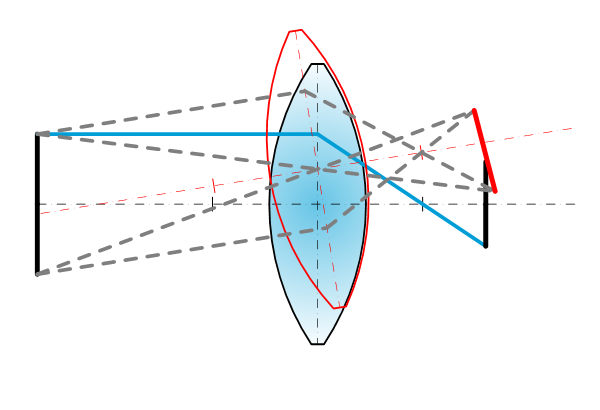
Lens x, lens, y, lens tilt, object tilt
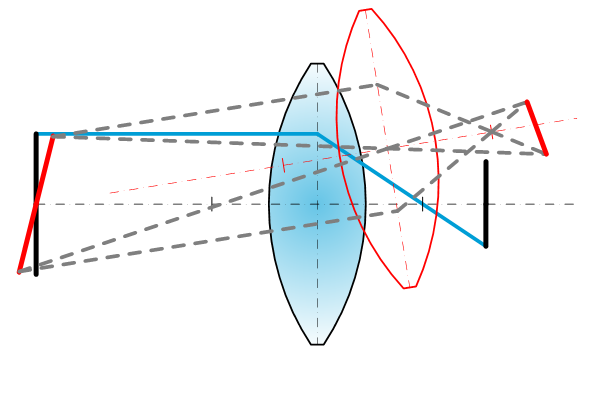
Lens y = object -y
Due to manufacturing also the incoming and outgoing radii of the lens can differ. Consequently, the focus distance is affected:
$\frac{1}{f}=\left(n-1\right)\left(\frac{1}{r_1}-\frac{1}{r_2}\right)$
