Introduction
This sheet provides the steps to compose a bode plot of an arbitrary ordinary differential equation. In the resulting bode plot some insights and interpretations are presented, which are also valid for frequency response functions.
Composition of bode
Step 1: Derive the (Ordinary) Differential Equation
$\ldots+\ m\ddot{x}+d\left({\dot{x}-\dot{x}}_{in}\right)+c\left(x-x_{in}\right)+\ldots=F_e$
Step 2: Laplace transform (using $x=x$, $\dot{x}=sx$, $\ddot{x}=s^2x$, …)
$\ldots+\ ms^2x+ds\left(x-x_{in}\right)+c\left(x-x_{in}\right)+\ldots=F_e$
Step 3: Transfer function (choose in and out) $H\left(s\right)=\frac{out\left(s\right)}{in\left(s\right)}$
$H(s)=\frac{x(s)}{x_{in}(s)}=\frac{ds+c+\ldots}{\ldots+ms^2+ds+c+\ldots}$
Step 4: Magnitude & Phase response $s=j\omega$, $j^2=-1$
$\left|H\right|=\sqrt{\left[Re\left(out\right)\right]^2+\left[Im\left(out\right)\right]^2}/\sqrt{\left[Re\left(in\right)\right]^2+\left[Im\left(in\right)\right]^2}$
$arg\left(H\right)=atan\left(\frac{Im\left(out\right)}{Re\left(out\right)}\right)-atan\left(\frac{Im\left(in\right)}{Re\left(in\right)}\right)$
Step 5: Bode plot, $f\left[Hz\right]=\frac{\omega}{2\pi}$
$A=\left|H\right|$ , $A[dB]=20log(A)$ , $A={10}^{A\left[dB\right]/20}$
$\varphi\left[deg\right]=\arg{\left(H\right)}\cdot\frac{180}{\pi}$
Magnitude plot: loglog($f,A$), phase plot: semilogx($f,\varphi$)
Magnitudes conversion
| dB | Gain | |
|---|---|---|
| -40 | ∼ | 1/100 |
| -20 | ∼ | 0.1 |
| 2 | ∼ | 1.26 (∼ +25 %) |
| 3 | ∼ | 1.41 (∼ +40 %) |
| 6 | ∼ | 2 |
| 20 | ∼ | 10 |
| 30 | ∼ | 30 |
| 40 | ∼ | 100 |
| 60 | ∼ | 1000 |
Slope & (Bode’s) gain/phase relation
Decrease in magnitude is related to phase lag: $\pm20dB/dec\sim\pm{90}^\circ$ phase shift for stable non-minimum phase systems -> effect of 1 pole or 1 zero.
Zeros ($z_i$) and poles ($p_i$):
$H=\frac{N\left(s\right)}{D(s)}=K\frac{\left(s-z_1\right)\left(s-z_2\right)\ldots\ (s-z_n)}{\left(s-p_1\right)\left(s-p_2\right)\ldots\ (s-p_m)}$
$z_1,\ldots.,\ z_n,p_1,\ldots,p_m$ obtained by factorization
Poles and zeros determine the asymptotic values in the bode plot.
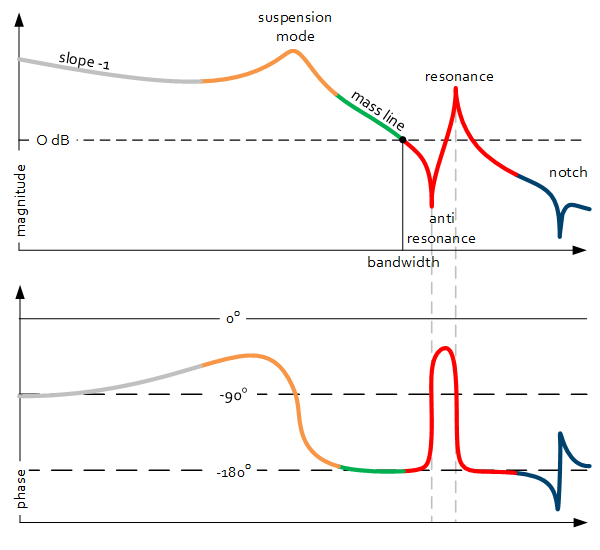
Slope -1 at low frequencies
If this is the case in the Bode plot of the controller, an integral action is present.
Suspension mode
Slope 0 with damped resonance followed by -2 slope in the low frequency range. Typical for suspension behavior in a motion system.
Mass line
The -2 slope part of the system response. The gain of the response equals the inverse mass of the system:
$H\left(s\right)=\frac{A}{s^2}=\frac{1}{ms^2}$
Complex poles/zeros (resonance/anti-resonance)
For complex (conjugate) poles and zeros, the gain/phase relation is doubled: $\pm40dB/dec\sim\pm{180}^\circ$ phase. The behavior around the complex poles/zero frequency is determined by the damping factor.
Notch filter
A special case of a complex pole zero pair is the notch filter, with more damping in the poles than in the zeros. The result is a dip (notch) in the response.
$H(s)=\frac{s+2\zeta_z\omega_n+\omega_n^2}{s+2\zeta_p\omega_n+\omega_n^2}$
Bandwidth (open-loop definition)
Zero-gain / 0 dB crossing in the open-loop Bode plot.
